Embark on a mathematical journey with course 1 chapter 2 fractions decimals and percents answer key, an invaluable resource designed to unlock your understanding of these fundamental concepts. This comprehensive guide provides clear explanations, step-by-step instructions, and a wealth of practice exercises to empower you in mastering fractions, decimals, and percents.
Delve into the intricate world of numbers as we explore the relationship between fractions and decimals, unravel the secrets of converting percents to fractions and vice versa, and conquer the challenges of performing operations on these diverse representations.
Course 1 Chapter 2: Fractions, Decimals, and Percents: Course 1 Chapter 2 Fractions Decimals And Percents Answer Key

This chapter introduces the concepts of fractions, decimals, and percents, and provides methods for converting between these different representations of numbers. It also covers the rules for performing operations (addition, subtraction, multiplication, and division) on fractions, decimals, and percents.
Fraction and Decimal Relationships
Fractions and decimals are two different ways of representing the same number. A fraction is a number that represents a part of a whole, while a decimal is a number that represents a part of a whole that can be divided into tenths, hundredths, thousandths, and so on.
To convert a fraction to a decimal, divide the numerator by the denominator. To convert a decimal to a fraction, write the decimal as a fraction with a denominator of 10, 100, 1000, and so on.
| Fraction | Decimal |
|---|---|
| 1/2 | 0.5 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
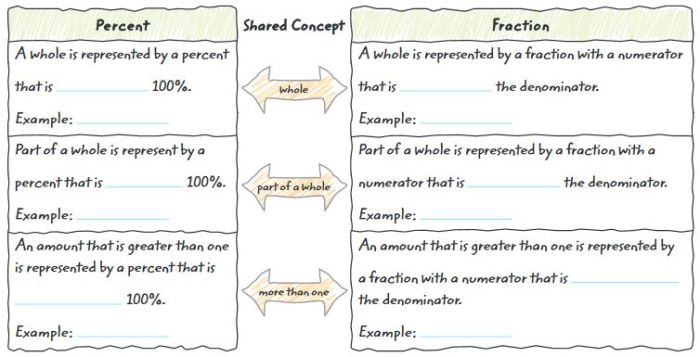
Percent as a Fraction and Decimal
A percent is a fraction or decimal that represents a part of a whole out of 100. To convert a percent to a fraction, divide the percent by 100. To convert a fraction to a percent, multiply the fraction by 100.
Percents are used in a variety of real-world applications, such as:
- Calculating discounts
- Measuring interest rates
- Calculating percentages of change
Operations with Fractions, Decimals, and Percents, Course 1 chapter 2 fractions decimals and percents answer key
The rules for adding, subtracting, multiplying, and dividing fractions, decimals, and percents are similar. However, there are some important differences to keep in mind.
| Operation | Fractions | Decimals | Percents |
|---|---|---|---|
| Addition | Find a common denominator and add the numerators. | Line up the decimal points and add. | Convert the percents to fractions or decimals and add. |
| Subtraction | Find a common denominator and subtract the numerators. | Line up the decimal points and subtract. | Convert the percents to fractions or decimals and subtract. |
| Multiplication | Multiply the numerators and the denominators. | Multiply the numbers as if they were whole numbers. | Convert the percents to fractions or decimals and multiply. |
| Division | Invert the second fraction and multiply. | Divide as if the numbers were whole numbers. | Convert the percents to fractions or decimals and divide. |
Applications of Fractions, Decimals, and Percents
Fractions, decimals, and percents are used in a variety of real-world applications, such as:
- Measuring ingredients in recipes
- Calculating discounts and sales tax
- Measuring distances and time
- Calculating probabilities and statistics
Question Bank
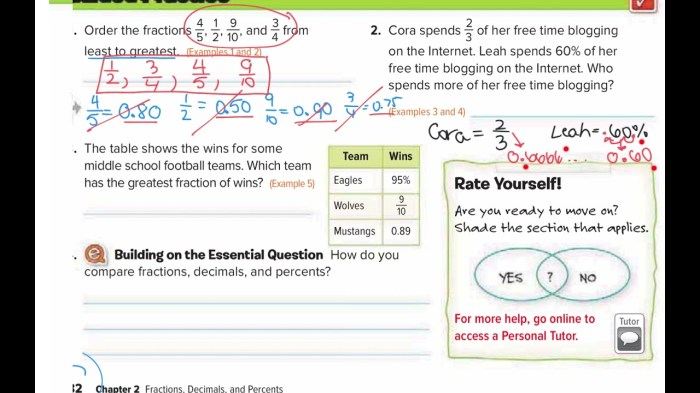
What is the relationship between fractions and decimals?
Fractions and decimals are two different ways of representing the same value. A fraction is a part of a whole, while a decimal is a number that is less than one and has a place value system based on powers of ten.
How do I convert a fraction to a decimal?
To convert a fraction to a decimal, divide the numerator by the denominator. For example, to convert 1/2 to a decimal, divide 1 by 2, which gives you 0.5.
How do I convert a percent to a fraction?
To convert a percent to a fraction, divide the percent by 100. For example, to convert 50% to a fraction, divide 50 by 100, which gives you 1/2.